• Measures magnetic parameters accurately
• Demagnetisation, eddy currents and sample cross-sectional area have been accounted for
• Capable of detecting the number of magnetic phase present in a sample

Introduction

A precise knowledge of various magnetic parameters of ferromagnetic substances, viz. coercivity, retentivity, saturation magnetisation and hysteresis loss, and ability to determine them accurately are important aspects of magnetic studies.

The information about the aforementioned properties can be obtained from a magnetic hysteresis loop which can be traced by a number of methods in addition to the slow and laborious ballistic galvanometer method. Among the typical representatives of AC hysteresis loop tracers, some require the ring form of samples while others can be used with thin films, wires or even rock samples. Ring form samples are not always practically convenient to make while in others demagnetisation effects sometime become quite important.

The present set-up can accept the samples of thin wires of different diameters. The demagnetisation effects, different diameters of samples and eddy currents (due to the conducting property of the material) has been taken into account within the design

Design Principle

When a cylindrical sample is placed coaxially in a periodically varying magnetic field the magnetisation in the sample also undergoes periodic variation. This variation is packed up by a coil placed coaxially with the sample.

For the uniform field Ha produced, the effective field H acting in the cylindrical sample will be

H = Ha-NM            or

H = Ha-NJ/µo  ...............................( 1 )

where M is magnetisation, N is normalised demagnetisation factor including 4p and J is the magnetic polarisation defined by

B = µoH + J

with B = m H or m 0(H+M) as magnetic induction. The signal corresponding to the applied field, Ha can be written as

e1=C1Ha ...................................... (2)

where C1 is a constant

Further the flux linking with the pick-up coil of area Ac due to sample of area As will be

Φ = µo(Ac-As)H' + AsB.

which under certain conditions reduces to

Φ = µoAcH + AsJ

The signal induced in the pick-up coil (e2) will be proportional to df/dt which after integration yields.

e3 = C3Φ = C3µoAcH + C3AsJ ........(3)

Solving (1), (2) and (3) gives

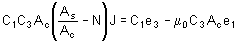
Based on these equations the electronic circuit has been designed to give values of J and H and hence the hysteresis loop. Further different magnetic phases present in the sample may also be identified by electronically manipulating the pick-up signal.